La profondeur de champ
- Notions fondamentales
- Explication de la profondeur de champ
- Calcul de la profondeur de champ
- Une technique bien utile: l'hyperfocale
Idéalement, tous les points d'un sujet devraient être nets sur la surface sensible. Mais cela n'est pas possible car le sujet est constitué d'une infinité de plans et les rayons de lumière correspondants convergent évidemment en avant ou en arrière du plan capteur. Pour cela, on appelle profondeur de champ toute la zone qui parait nette pour l'½il.
Dans les explications qui suivront, on se placera, comme pour la mise au point, dans le cadre de l'optique de Gauss pour négliger tous les défauts des lentilles et leurs conséquences sur l'image finale. De plus, on ne considérera encore qu'une seule lentille pour simplifier.
Notions fondamentales
Le diaphragme
Dans un objectif, le diaphragme est un ensemble de lamelles amovibles formant un cercle (en réalité un polygone) de diamètre différent en fonction de leurs positions. Ce cercle, plus ou moins ouvert, influera sur deux paramètres principaux: la quantité de lumière qui sera amenée à passer et la profondeur de champ. Le diaphragme est aussi acteur de différentes aberrations qui ne seront pas étudiées ici.
L'ouverture du diaphragme est notée assez spécialement; La quantité de lumière le traversant ayant un rapport avec la focale de l'objectif, il a été décidé d'exprimer l'ouverture en fonction de cette focale. Le diamètre de l'ouverture est donc notée f/x, ou x est un nombre et f la focale de l'objectif. De cette manière, une ouverture de f/1.4 ne correspondra pas toujours au même diamètre mais laissera toujours passer la même quantité de lumière. Une conséquence de cette notation est que plus le nombre x sera grand, plus l'ouverture sera petite.

Un diaphragme
Le cercle de confusion
Le cercle de confusion a un rapport direct avec la résolution de notre ½il. Il correspond au diamètre maximal que l'image d'un point à l'intérieur de notre ½il doit avoir pour que ce point nous paraisse net. Le diamètre de ce cercle est constant pour un ½il donné. Il est en rapport direct avec le diamètre de confusion: ce dernier correspond au diamètre maximal qu'un point peut avoir sur une image pour qu'il nous paraisse net. Ce diamètre augmente si l'on éloigne l'image de l'oeil, il diminue si l'on approche l'image. La profondeur de champ dans une image correspond à toute la zone ou le diamètre des points sera inférieur au diamètre de confusion. Elle augmente donc quand on éloigne l'image et diminue lorsqu'on approche l'image.
Explication de la profondeur de champ
Le premier schéma représente quatre rayons émis par le point O à travers un diaphragme fortement ouvert. Le deuxième représente ces mêmes quatre rayons à travers un diaphragme bien plus fermé.

Schéma 1: Le diaphragme est ouvert
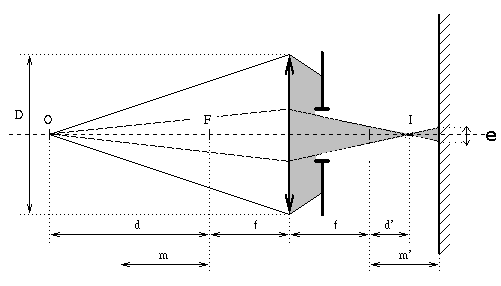
Schéma 2: Le diaphragme est fermé.
Sur ces deux schémas, deux choses sont conséquences de la fermeture du diaphragme : L'ouverture qui laisse passer la lumière étant plus fermée sur le schéma 2, une partie des rayons sont bloqués, ils n'atteindront jamais le capteur, contrairement au schéma 1 ou tous les rayons représentés atteignent le capteur. La deuxième, conséquence de la première, se voit aisément en comparant les deux schémas: quand le diaphragme est fermé, le diamètre de confusion e est plus petit. En conséquence, il est facilement concevable que cette tache sera considérée comme acceptable par l'½il humain sur une profondeur plus élevée.
La profondeur de champ augmente lorsque le diaphragme se ferme, cependant, ce dernier laissant passer moins de lumière, le temps pendant lequel le capteur devra être exposé pour une même luminosité sera supérieur.
Pour conclure voilà deux photos, sur celle de droite (diaphragme fermé), la profondeur de champ est grande. Elle l'est moins sur celle de gauche (diaphragme ouvert)
 |
 |
| Diaphragme ouvert | Diaphragme fermé |
Calcul de la profondeur de champ
Le diamètre de confusion e le plus couramment accepté est de 0.03mm (sur l'image d'un capteur plein format), ce diamètre est le diamètre maximal d'une tache que notre ½il considérera nette si l'image est regardée à une distance égale à la diagonale de cette dernière. Ce sera donc celui qui sera choisi ci-après.
Le diamètre de confusion e le plus couramment accepté est de 0.03mm (sur l'image d'un capteur plein format), ce diamètre est le diamètre maximal d'une tache que notre ½il considérera nette si l'image est regardée à une distance égale à la diagonale de cette dernière. Ce sera donc celui qui sera choisi ci-après.
- D = distance sujet/objectif
- f = ouverture du diaphragme
- F = focale de l'objectif
- n = netteté angulaire c'est à dire e/f


En isolant les deux limites, il est facile de les calculer.


Calculons maintenant la profondeur de champ de deux même scène avec un diaphragme différent. On estime que l'on est à 2m du sujet, la focale de notre objectif est de 50mm (0.05m). La netteté angulaire est de 1/1500 pour un diamètre de confusion de 0.03mm. Pour le premier calcul, on ouvre à f/1,4, pour le deuxième on ouvre à f/16.


Pour une ouverture f/1.4, on constate que la profondeur de champ s'étend, pour un cercle de confusion de 0.03mm de 1.93m à 2.07m.
Passons maintenant à une ouverture du diaphragme bien plus petite : f/16.


Dans ce cas, la profondeur de champ s'étend, toujours pour le même diamètre de confusion, de 1.40m à 3.49m
Ces calculs mettent en évidence le fait que, lorsque l'ouverture du diaphragme diminue (chiffre plus élevé), la profondeur de champ augmente. Ceci confirme nos schémas.
On admet très souvent que la profondeur de champ varie en fonction de la focale, à tort. En effet elle varie avec le grandissement. En effet, ce dernier ne dépend pas seulement de la focale, mais aussi de la distance de mise au point. Si un sujet à une taille de un centimètre sur le capteur, le fait qu'il soit pris avec un 1200mm ou un 50mm ne changera rien à la profondeur de champ.
De plus, la profondeur de champ est toujours plus grande derrière le sujet que devant. Cette différence est minime à grande ouverture ou à fort grandissement (focale longue et distance de mise au point faible) mais apparaît très nettement lorsque l'on ferme le diaphragme ou que le grandissement est faible. (La prise de paysage en est un excellent exemple).
Une technique bien utile: l'hyperfocale
Pour un diaphragme donné, la distance hyperfocale est la distance de mise au point minimale de telle sorte que la profondeur de champ s'étende jusqu'à l'infini et que la limite antérieure de la profondeur de champ soit la plus grande possible.
Par exemple, on veut photographier un homme devant une montagne à focale et ouverture donnée. La distance hyperfocale sera la distance minimale à laquelle le photographe devra se placer de l'homme pour pouvoir effectuer la mise au point sur la distance H de façon à avoir la montagne et l'homme net.
La formule de l'hyperfocale est définie par:
- H: distance hyperfocale
- F: focale
- f: ouverture
- e: diamètre de confusion

En appliquant cette formule, on se rend compte que la distance hyperfocale diminue avec des diaphragmes plus fermés et des focales courtes. Ce qui correspond aux évolutions de la profondeur de champ en fonction de la focale et du diaphragme.
Voici un exemple de calcul de l'hyperfocale.
- F= 50 mm = 0.05m (focale)
- f = 16 (ouverture)
- e = 0.03mm = 0.00003m (diamètre de confusion)

Si l'on reprend notre exemple, dans ce cas, l'homme devra être à 5.2m du photographe pour que l'homme et tout ce qu'il y a derrière lui soit net.